线性回归

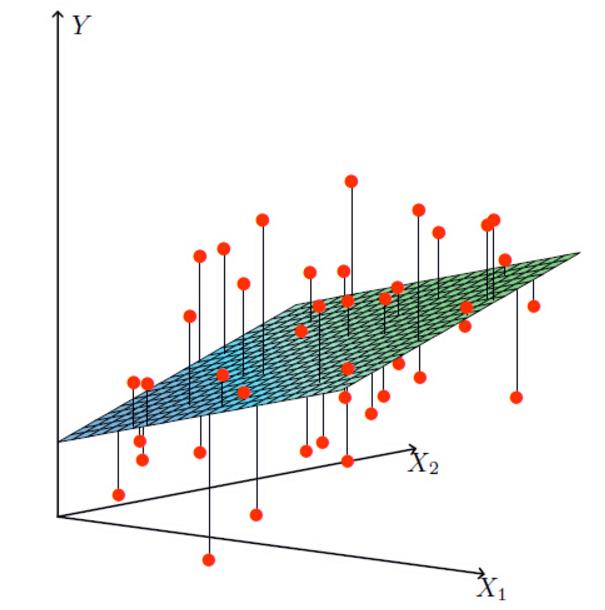
$$
\begin{aligned}
h_\theta(x) &= \theta_{0} + \theta_{1}x_{1} + \theta_{2}x{2} + … + \theta_{n}x_{n} \\
&= \sum_{i=0}^{n}\theta_ix_i\\
&= \theta x
\end{aligned}
\tag{1}
$$

真实值和预测值之间存在差异，用$\epsilon_i$表示误差，则对于每个样本有:

$$
\begin{aligned}
y^{(i)}=\theta^Tx^{(i)} + \epsilon^i
\end{aligned}
\tag{2}
$$

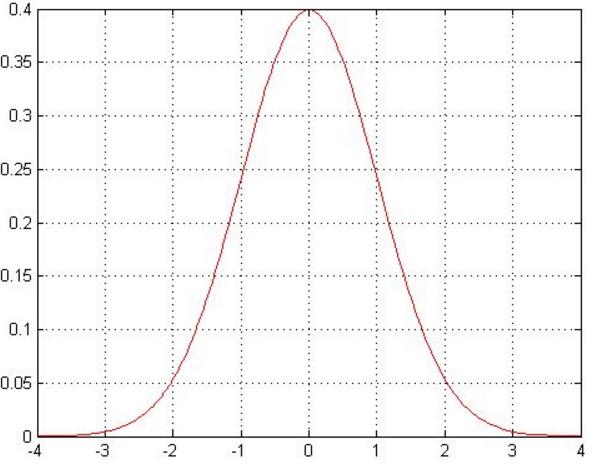
误差$\epsilon^{(i)}是独立同分布的，假定服从均值未0，方差为\theta^2$的高斯分布

预测值与误差关系为：

$$
\begin{aligned}
y^{(i)}=\Theta^Tx^{(i)} + \epsilon^i
\end{aligned}
\tag{3}
$$

$$
\begin{aligned}
p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\epsilon^{(i)})^2}{2\sigma^2}}
\end{aligned}
\tag{4}
$$

将$(3)$带入$(4)$，可得:

$$
\begin{aligned}
p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}
\end{aligned}
\tag{5}
$$

构造似然函数，使得什么样的参数$\theta$跟数据组合后为真实值的概率最大。

$$
\begin{aligned}
L(\theta) &= \prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta) \\
&= \prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}}
\end{aligned}
\tag{6}
$$

使用对数似然，将乘法转换为加法，

$$
\begin{aligned}
logL(\theta) = log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}}
\end{aligned}
\tag{7}
$$

展开化简:

$$
\begin{aligned}
logL(\theta) &= \sum_{i=1}^mlog\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}} \\
&= mlog\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^m(y^{(i)} - \theta^Tx^(i))^2
\end{aligned}
\tag{8}
$$

为了让对数似然函数越大越好，则使得(8)式越小越好, (最小二乘法):

$$
\begin{aligned}
J(\theta) &= \frac{1}{2} \sum_{i=1}^m(y^{(i)} - \theta^Tx^{(i)})^2 \\
&= \frac{1}{2} (X\theta - y)^T(X\theta - y)
\end{aligned}
\tag{9}
$$

对公式(8)关于$\theta$求偏导:

$$
\begin{aligned}
\nabla_\theta J(\theta)
&= \nabla_\theta (\frac{1}{2} (X\theta - y)^T(X\theta - y)) \\
&= \nabla_\theta (\frac{1}{2} (\theta^TX^T - y^T)(X\theta - y)) \\
&= \frac{1}{2} (2X^TX\theta-X^Ty-(y^TX)^T) \\
&= X^TX\theta-X^Ty
\end{aligned}
\tag{10}
$$

令偏导数为0，则有公式(10)：
$$
\begin{aligned}
\theta = (X^TX)^{-1}X^Ty
\end{aligned}
\tag{11}
$$